Which geometry is better to travel in?
The simplest non-trivial setting to analyse this question
in a stochastic setting is that of the Laplace-Beltrami operator
in a tubular neighbourhood of an infinite curve
in a two-dimensional surface,
subject to Dirichlet boundary conditions.
In my paper with Martin Kolb
[
Journal of Spectral Theory (2014)],
we argue (based on the large-time behaviour of the heat equation)
that it is the negative/positive ambient curvature
which is good/bad for the Brownian motion
(mathematically, due to the existence of Hardy-type inequalities
or discrete spectra, respectively).

Non-self-adjoint spectral theory
Studying non-self-adjoint operators is like being a vet rather than a doctor: one has to acquire a much wider range of knowledge, and to accept that one cannot expect to have as high a rate of success when confronted with particular cases.
[Brian Davies (2007)]
This very pertinent judgment has been a leitmotif
for my research on spectral and pseudospectral properties
of non-self-adjoint operators in quantum mechanics and elsewhere.
It has also been a motto for the
conference series,
which I have been organising
with Lyonell Boulton and Petr Siegl
in various places in Europe and America since 2010.
To me, the transfer from the self-adjoint paradise
to non-self-adjoint torments
was like opening Pandora's box...
 Arthur Rackham: Pandora's box
Arthur Rackham: Pandora's box
An important success with particular cases
is given by my paper with Luca Fanelli and Lucrezia Cossetti
[Communications in Mathematical Physics (2020)],
where we develop the method of multipliers
to obtain absence of eigenvalues of
relativistic operators of Pauli and Dirac types.
The case of Schrodinger operators with complex potentials
is covered by my papers with Luca Fanelli and Luis Vega
[Journal of Spectral Theory &
Journal of Functional Analysis (2018)].
In my papers with Petr Siegl and Tho Nguyen Duc
[
Journal of Functional Analysis (2019 & 2022)],
we develop a first systematic construction of non-semi-classical
pseudomodes for Schrodinger and Dirac operators.
We cover discontinuous potentials,
solving thus an open problem from a
2015 AIM workshop.
Quasi-self-adjoint quantum mechanics
In my (most cited) paper with Petr Siegl
[Physical Review D (2012)],
we disprove quasi-self-adjointness of
the imaginary cubic (or Bender's) oscillator.
More specifically, we establish the existence
of a generalised metric operator
(based on the completeness of eigenfunctions)
which is however necessarily singular
(due to the absence of Riesz-basis property).
In another highly cited paper
[Journal of Physics A (2006),
with Hynek Bila and Miloslav Znojil],
I introduce a new class of quasi-self-adjoint toy models:
The operator acts as
the one-dimensional Laplacian and the non-self-adjointness
is introduced via complex Robin boundary conditions only.
The simplicity allows for closed formulae of the metric operator
as well as of the self-adjoint Hamiltonian.
At the same time, the multidimensional generalisations
lead to peculiar spectral properties.
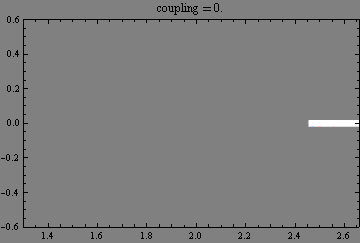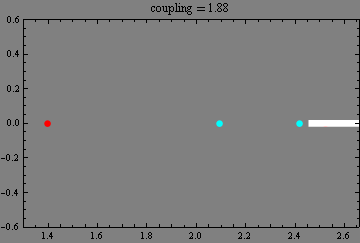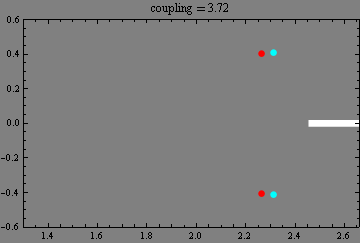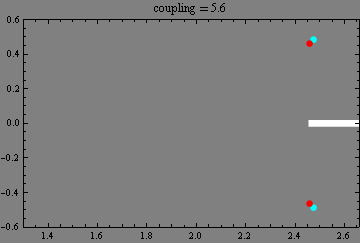
|
Eigenvalues in a waveguide with complex Robin boundary conditions.
The emergence of real eigenvalues (blue and green balls)
and complex conjugated pairs of eigenvalues (red and cyan balls)
from the continuous spectrum (thick white line)
and their trajectories (with apparent collisions) in the complex plane
as a boundary coupling parameter increases.
(Collaboration with Milos Tater.)
|